Back

Where's the tree in Fenwick tree?

December 2019

If you've ever read about Fenwick trees, you've probably wondered where the tree that they speak of was at. You've probably also wondered what on earth would motivate someone to come up with those bitwise gimmicks that magically solves a difficult problem. The answer is rooted (no pun intended) at the indices of a typical full binary search tree.

So the problem is to process two kinds of queries fast on an array $a$ of size $n$ initialized to zeroes.

Add some number $v$ to $a_p$.
Return the sum $a_1+a_2+\cdots+a_p$.

Let's look at a solution that's kinda similar to a typical divide and conquer approach that segment trees follow. Consider the array $$a=[11,~7,~14,~15,~1,~12,~5,~3,~6,~13,~9,~2,~4,~10,~8]$$ of size $n=15$. We'll construct a full binary search tree on its indices ${1,2,...,15}$.

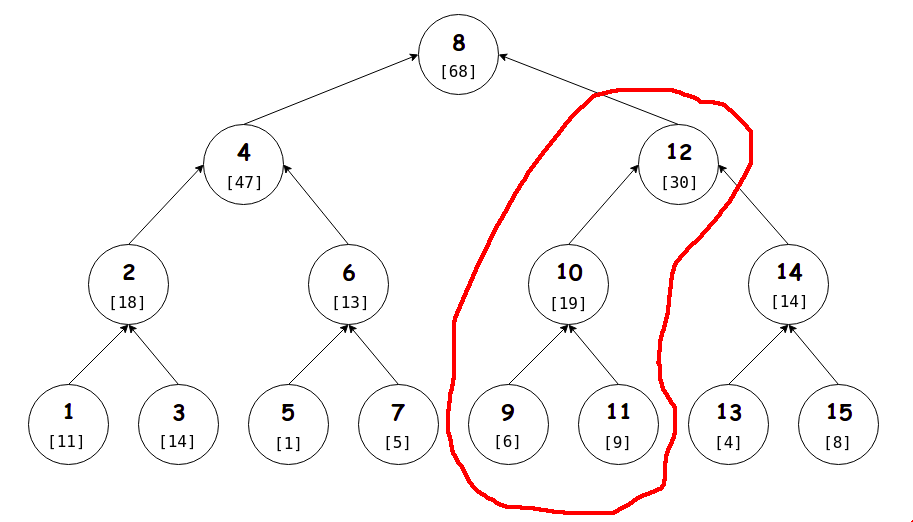
We keep at each vertex the sum of values at all indices in its left subtree and itself. For instance, the red region in the image shows the relevant indices for vertex $12$. The corresponding sums for array $a$ are written within brackets. Some examples:

Value at vertex $7$ is simply $a_7=5$.
Value at vertex $12$ is $a_9+a_{10}+a_{11}+a_{12}=30$.
Value at vertex $8$ is $a_1+a_2+\cdots+a_8=68$.

There you go! What you're looking at is a Fenwick tree built on the array $a$. Let's observe how we can perform updates and retrieve sums.

If we were to compute $a_1+\cdots+a_{11}$ then we'd start at the vertex $11$ and climb up to the root collecting values of vertices that cover some of our desired range. These are exactly the vertices with indices not greater than $11$.

Initially we're at vertex $11$ which is not bigger than $11$, so we collect the sum $9$ and climb up.
Now we're at vertex $10$ which is not bigger than $11$, so we collect the sum $a_9+a_{10}=19$ and climb up.
Now we're at vertex $12$ which actually is bigger than $11$, so we do nothing and climb up.
Now we're at the root $8$ which is not bigger than $11$, so we collect the sum $a_1+\cdots+a_8=68$ and finish with $9+19+68=96$, which is our desired answer.

How about adding $69$ to $a_5$? We perform a similar climb from vertex $5$ adding $69$ to the vertices that cover $a_5$. These are exactly the vertices with indices at least $5$.

Initially we're at vertex $5$, which definitely covers $a_5$. So we add $69$ to it and climb up.
Now we're at vertex $6$ which is bigger than $5$, so it covers $a_5$. We add $69$ to it and climb up.
Now we're at vertex $4$ which is smaller than $5$, so this vertex doesn't get affected. We do nothing and climb up.
Finally we're at the root $8$ which is bigger than $5$, so it covers $a_5$. We add $69$ to it and finish our tour.

Clearly these operations take time proportional to the height of the tree. And since we've constructed a full binary search tree, the height and thus the runtime, is $\mathcal{O}(\lg n)$.

It remains to look closely at the vertex indices of a full binary search tree to further optimize this process. We naturally look at the binary representations of the indices.

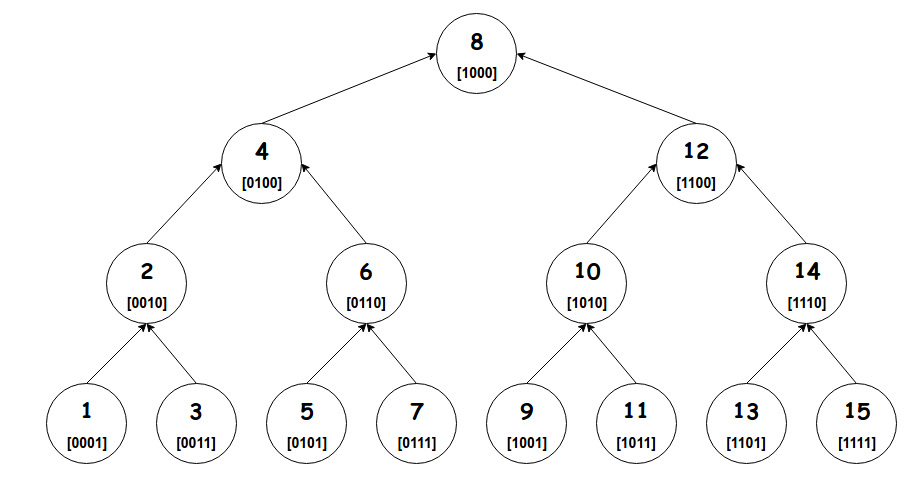
Here's a cool observation (try proving it maybe):

When we move from a child $u$ to its parent, the last 1 (from left) in the binary representation of $u$ moves one step to the left (and possibly merges with another 1 if there is already one).

Let's call this operation a shift. So a shift transforms a vertex to its parent. For instance, vertex $11$ (1011) has parent $10$ (1010), which in turn has parent $12$ (1100). Equipped with this, we can revisit our algorithms to retrieve sums and perform updates.

In order to compute $a_1+\cdots+a_{11}$ we need to collect sums at vertices on the way from vertex $11$ to root that have indices at most $11$. But notice that a shift decreases the original value if there's a merge happening, and increases the value otherwise. For example: 1010 transforms into 1100 after a shift which is bigger. But 1011 transforms into 1010 after a shift which is smaller - this is because the last 1 merges with the one on its left and thus, essentially vanishes. We can utilize this observation to skip all the shifts without merges and move to the next merge: 1101 -> 1110 -> 1100 simplifies into 1101 -> 1100. This is essentially removing the last 1 bit: 1101 - 0001 = 1100. So our algorithm looks like this: start at vertex $11$, collect sum, remove last 1, repeat (till root).

In order to add $69$ to $a_5$ we need to update all vertices on the way from vertex $5$ to root that have indices at least $5$. We recall the observation that a shift decreases the original number if there's a merge happening, and increases otherwise. So we need to skip all the shifts with merges and move to the next shift without merge: 1011 -> 1010 -> 1100 simplifies into 1011 -> 1100. This is essentially adding to the last 1 bit: 1011 + 0001 = 1100. So our algorithm looks like this: start at vertex $5$, add value, add to the last 1, repeat (till root).

And finally, let's look at a trick to isolate the last 1 bit in a number x: it is given by x & -x. Here's why: let's write the number as x = a10..0 where the 1 is the last one in x. Then -x is found by inverting all bits in x and adding 1 (two's complement). We get -x = b01..1 + 1 = b10..0 where b is found by inverting all bits of a. So x & -x = (a10..0) & (b10..0) = 0..010..0 with only the last 1 bit of x retained at its position.

Combining all this, we get the following simple procedures that take up $\mathcal{O}(n)$ memory in whole and $\mathcal{O}(\lg n)$ time per query.

  void add (int p, int v) {
    while (p <= n) a[p] += v, p += p & -p;
  }

  int sum (int p) {
    int ret = 0;
    while (p) ret += a[p], p -= p & -p;
    return ret;
  }